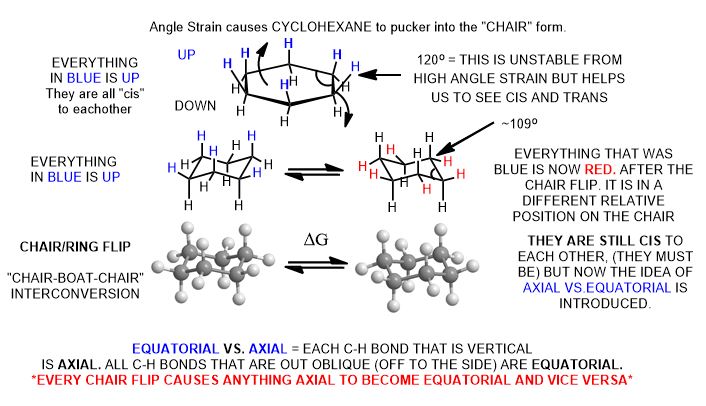
Chair Cyclohexane
The Flipping Chair
Chair Cyclohexane Conformers
(Chair-Boat-Chair Interconversion)
You should expect some variant of the following question:
Draw the most stable conformational isomer of trans-1,4-diethylcyclohexane.
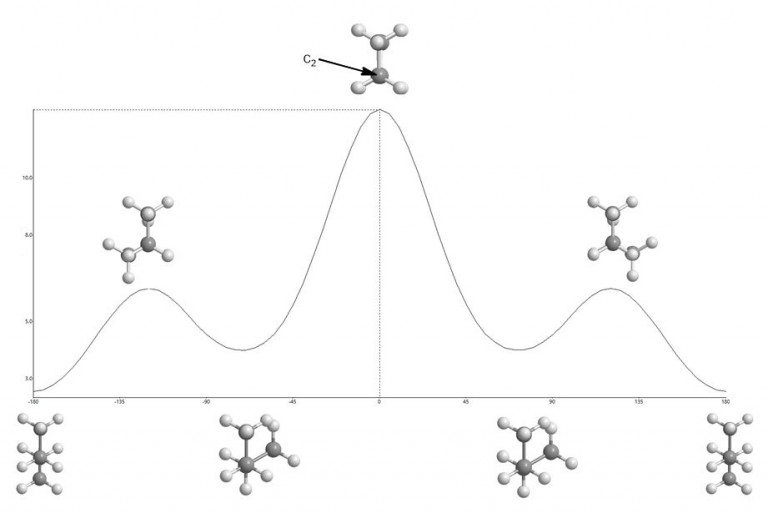
So far you’ve looked at the energy diagrams of molecules in different shapes or conformations using what are known as Newman Projections. This is n-butane in its most stable conformation. The terminal methyl groups are as far apart as possible. This conformation occupies the bottom of the energy profile at both ends of the graph below through 360 degrees of rotation. Starting from the far left of the energy diagram below (anti) and rotating there are various peaks and troughs until one returns back to the anti conformation on the far right of the profile. Peaks are eclipsed conformations and troughs are staggered conformations.
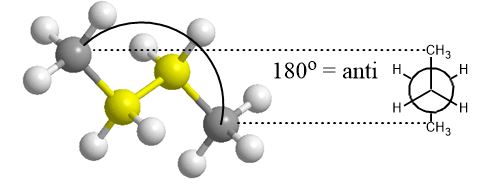
The point of a Newman projection is to look at the dihedral angle between 4 of the carbons while rotating the C2-C3 single bond in yellow and viewing (in your mind’s eye) or focusing on the one of the internal carbons only. You would see one carbon head-on with an understanding that the carbon behind is there but not visible (eclipsed) by the one in front of it.
Newman Projections
In this projection, you see the carbon you look at carbon 2 and it’s attached to carbon 3 which you can’t see. Thus, one eclipses the other in the Newman Projection and all you see of the rear carbon are the bonds extending from it. For any two sp3 (tetrahedral) carbons this can be done and will be asked of you.
It becomes obvious that as the angle between those groups gets smaller, by rotating the bond between c2 and c3, the potential energy increases. Van der Waals repulsion (steric hindrance) plays a role in making this conformation unfavorable since it means an increase in potential energy. This is a “steric” effect. The alkene (Z)-2-butene has a non-rotatable bond and is locked this way. When the methyl groups eclipse each other in vicinal carbons (1,2-relationship), at an energy maximum, this is also referred to as an A(1,2) interaction or strain.
Generally atoms and groups don’t like to be anywhere closer than they have to be. You know that already. It is not only steric hindrance but also stereoelectronics which involves the orbitals around atoms and the interactions between them. For the time being, explanations about how certain reactions occur will be limited to steric arguments because they are sufficiently obvious.
Things can always be made more complicated (let’s avoid that). Reminiscent of VSEPR theory (the maximization of angle geometry for bonds around single atoms), conformational analysis studies these kinds of interactions between atoms.
Conformational Isomers Have Different Energies
The energy of the system is at its lowest when groups are spread out as far as possible as is associated with favorable atomic orbital interactions. This means when the bonds are staggered this also gives the best alignment of orbitals (including the atomic anti-bonding orbitals). This is one type of electron delocalization which is discussed later in second semester.
Gauche interactions (60o relationships between groups larger than hydrogen) occupy energy troughs but are obviously higher in energy than the anti conformation where they are furthest apart. Clearly, they still occupy local energy minima since they are staggered.
- These are the staggered conformers (the energy wells or minima) that have the largest (here, methyl) groups 60o apart. They are gauche with respect to one another).
- Eclipsed bonds are local maxima and syn-butane (the two largest groups are eclipsed) in the center is the absolute maximum.
What is this 60o relationship in a dihedral angle is called? It’s a French word…”gauche” meaning left or more appropriately, skewed. Its English usage has more personal connotations…
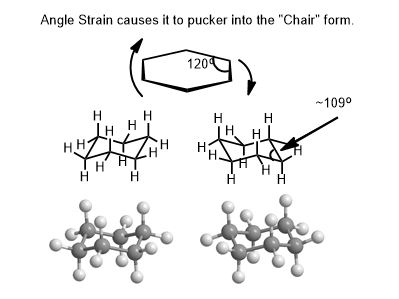
The Chair Conformation is Most Important
While staggered, gauche is still higher energy and therefore not as favorable as anti (180o)
Sometimes the ring is intentionally drawn in a planar structure to expose what is cis and what is trans (on one face of the ring or the other) for clarity.
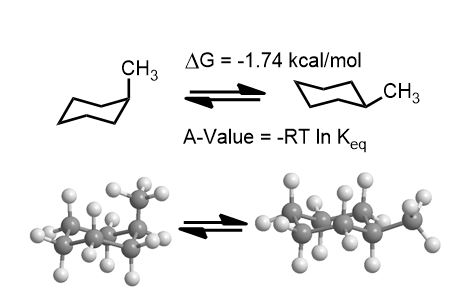
The terms axial and equatorial are unlike cis and trans. They are not fixed but depend on whether the ring has gone interconversion by a chair-boat-chair transition (ring-flip) which involves a change in free energy. Thermodynamic stability depends on ΔG = -RT ln Keq. Since Keq is the ratio of one conformer versus the other, ΔG is large and negative when you avoid large substituents in the axial (unfavorable) conformation for that group.
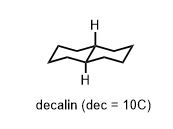
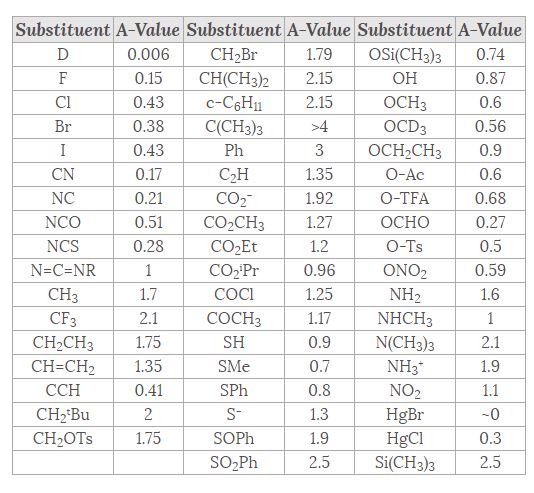
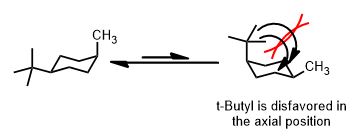
There is a very useful table of the energies of substituent groups in the axial versus equatorial position. They are known as “A-Values” where the A comes from “axial” and over time, you will just spot them. They are easy-to-handle numbers like 1.7, 1.8, 2.1 kcal/mol (Me, Et, i-Pr respectively). 5.4 for t-butyl (C(CH3)3). That is substantial. A t-butyl group is large enough to prevent chair flipping by acting as anchor against it. The energy difference is as large enough to be similar to the corresponding chair flip in decalin.
Link: (attribution: Hans Reich; Univ. of Wisc.); Table courtesy of Wikipedia.com
Their source lists t-Butyl (C(CH3)3) as “>4” kcal/mol. This is enormous. Other credible tables list it more accurately as 5.4 kcal/mol. The 1,3-diaxial interactions (two gauche interactions) of t-butyl if it became axial are shown. This is one good use of a model.
For example, methylcyclohexane below has two conformations one that is favored over the other by a free energy difference of 1.7 kcal/mol. That it has a negative value is a given. It is written as a spontaneous process. (-ΔG). Nevertheless, remember that absolute values of ΔG are used.
Here’s an example of the logic:
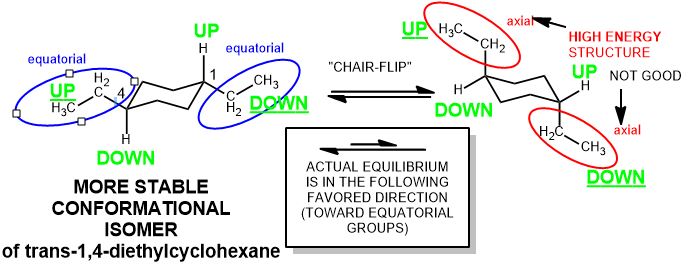
Draw trans-1,4-diethylcyclohexane in both chair conformations and indicate the most stable chair.
- First you draw the compound in 2D. You want to understand what you’re working with an have a feeling of consistency. If I draw out 1,4-diethylcyclohexane, I get two chairs.
- One is energetically not feasible at equilibrium and the other is the same compound but in a form that’s more stable—it has greater stability—(3.8 kcal/mol) better (this is no small energy difference) and means that each axial ethyl group has two gauche interactions with the ring (1,3-diaxial interactions): (ΔGo=1.9 kcal/mol). And that is the case.
- If you have problems converting the structure from 2-D to 3-D, it’s a matter of which side of the ring the group is on (up or down). Do not expect to be making cis and trans relationships if you try to correlate the idea of togetherness or oppositeness with the transitory phenomenon of being axial or equatorial. Axial and equatorial are temporary and treated as an equilibrium. It depends which conformation the chair happens to be at a particular time-average. On the other hand, cis and trans doesn’t change. So it the groups are all wedges, they are all “up” (or all “down”) with respect to the ring.
- Each group that is axial has two gauche interactions [1,3-diaxial interactions] with the chair 2 carbons away in both directions. These gauche interactions are destabilizing. There is a corresponding table of A-values depending on how large an effect this group has on equilibrium flipping of the chair.
- Axial is higher energy, and the larger the group, the less likely the chair is found in that conformation, on average.
Solution:
Add up the A values, here 1.8 + 1.8 kcal/mol (from A-value table) is a 3.6 kcal/mol difference in energy in the reverse direction.
Question: Draw the most stable conformational isomer of (trans)-1-isopropyl-3-methylcyclohexane.
First draw it 2D. Then?
Solution in the forum.

Leave a Reply
You must be logged in to post a comment.